
Сетчатый купол планетария завода Carl Zeiss
Йена, 1913-24 гг.
Инженер: Вальтер Бауэрсфельд
Производитель: Завод Карл Цейс
Йена, 1913-24 гг.
Инженер: Вальтер Бауэрсфельд
Производитель: Завод Карл Цейс
МАРШ — Технологии. ВА2 2019-2020.
Андрей Астахов, Федор Большаков, Александра Гаврилова, Софья Добычина, Виктория Денисова, Анна-Мария Степанова
Андрей Астахов, Федор Большаков, Александра Гаврилова, Софья Добычина, Виктория Денисова, Анна-Мария Степанова
Сетчатый стальной купол, возведенный на крыше фабрики Карла Цейса в Йене в 1924 г. стал первым геодезическим куполом в мире, предвосхитив развитие сетчатых куполов Фуллера на 40 лет. В ходе исследования мы изучили конструкцию с точки зрения ее роли в истории развития куполов и мембранных оболочек, ознакомились с принципом ее геометрического построения, построили цифровую модель конструкции, используя Rhinoceros, а также произвели конструктивные расчеты с помощью расширений Grasshopper и Karamba 3D.
КОНТЕКСТ
Сетчатый купол был возведен в 1920-х гг. на крыше оптико-механического завода в Йене, основанного, как мастерская по производству точной оптики, немецким изобретателем Карлом Цейсом в 1846 году.
Руководил проектом инженер завода Вальтер Бауэрсфельд. Он же автор идеи самого планетария, как системы, состоящей из взаимно дополняющих друг друга проекционного устройства и сферического проекционного экрана (купола).
Сетчатый купол был собран из металлических стержней прямоугольного сечения 20*8 мм и покрыт впоследствии торкретированным бетоном для создания идеального сферического проекционного экрана. Соотношение веса и диаметра мембранного купола-оболочки стало революционным, и, согласно расчетам, с увеличением пролета строительство таких куполов становилось еще более выгодным.
Сетчатый купол был возведен в 1920-х гг. на крыше оптико-механического завода в Йене, основанного, как мастерская по производству точной оптики, немецким изобретателем Карлом Цейсом в 1846 году.
Руководил проектом инженер завода Вальтер Бауэрсфельд. Он же автор идеи самого планетария, как системы, состоящей из взаимно дополняющих друг друга проекционного устройства и сферического проекционного экрана (купола).
Сетчатый купол был собран из металлических стержней прямоугольного сечения 20*8 мм и покрыт впоследствии торкретированным бетоном для создания идеального сферического проекционного экрана. Соотношение веса и диаметра мембранного купола-оболочки стало революционным, и, согласно расчетам, с увеличением пролета строительство таких куполов становилось еще более выгодным.

Сборка сетчатого купола на крыше фабрики Карла Цейса, 1922, Архив Института Легких Конструкций (ILEK)
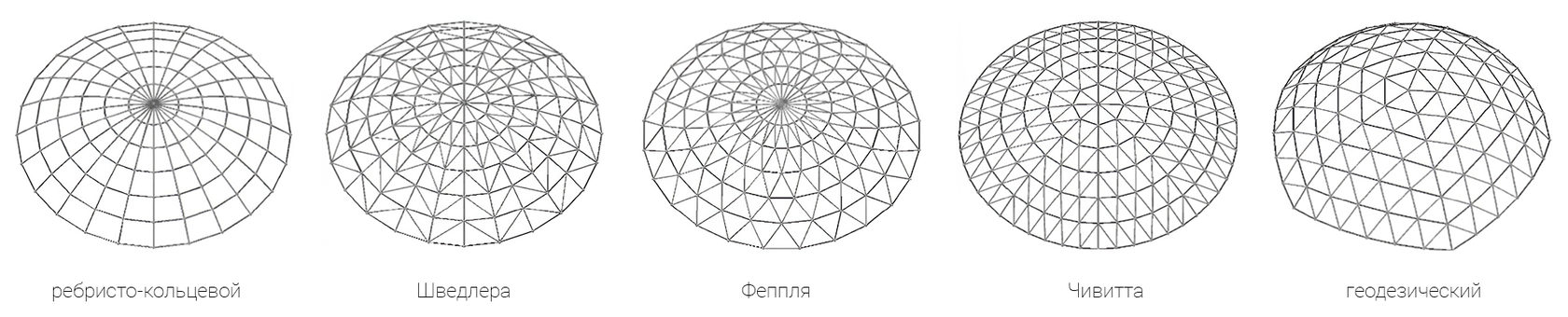
Типы куполов. Источник: Yan et al., Mechanism of coupled instability of single-layer reticulated domes, 2016
ПОСТРОЕНИЕ СЕТЧАТОГО КУПОЛА
В 1879 году немецкий инженер Иоганн Вильгельм Шведлер впервые предложил теорию расчета купола как пространственной конструкции. В отличие от ребристо-кольцевых куполов, рассчитываемых как плоскостные системы по меридиональным сечениям, купол Шведлера представляет собой пространственно работающую статически определимую конструкцию, собранную из меридиональных, кольцевых и диагональных элементов, образующих жесткий (треугольный) каркас.
Новая система значительно уменьшала вес конструкции (до 30 %), упрощала сборку и позволяло значительно увеличить пролеты (до 62м). Купола Шведлера пользовались большой популярностью как в Европе, так и России вплоть до начала XX века.
На ранних этапах развития сетчатых конструкций, (системы Шведлера и Феппля) купола имели центрально-симметричную конструкцию,
В 1879 году немецкий инженер Иоганн Вильгельм Шведлер впервые предложил теорию расчета купола как пространственной конструкции. В отличие от ребристо-кольцевых куполов, рассчитываемых как плоскостные системы по меридиональным сечениям, купол Шведлера представляет собой пространственно работающую статически определимую конструкцию, собранную из меридиональных, кольцевых и диагональных элементов, образующих жесткий (треугольный) каркас.
Новая система значительно уменьшала вес конструкции (до 30 %), упрощала сборку и позволяло значительно увеличить пролеты (до 62м). Купола Шведлера пользовались большой популярностью как в Европе, так и России вплоть до начала XX века.
На ранних этапах развития сетчатых конструкций, (системы Шведлера и Феппля) купола имели центрально-симметричную конструкцию,
что приводило к увеличению плотности элементов в верхней центральной зоне и неравномерному распределению материала.
В секторально-сетчатом куполе, или куполе Чивитта более равномерное деление на элементы достигалось за счет разбивки поверхности на 8 секторов, состоящих из кольцевых и диагональных соединений. Наконец, вершиной развития сетчатых купольных конструкций стал геодезический купол, изобретенный Вальтером Бауэрсфельдом при создании планетария. О в отличие от предыдущих систем, принцип его построения основан на геодезическом подразделении сферы и может применяться только для создания идеально-сферических куполов.
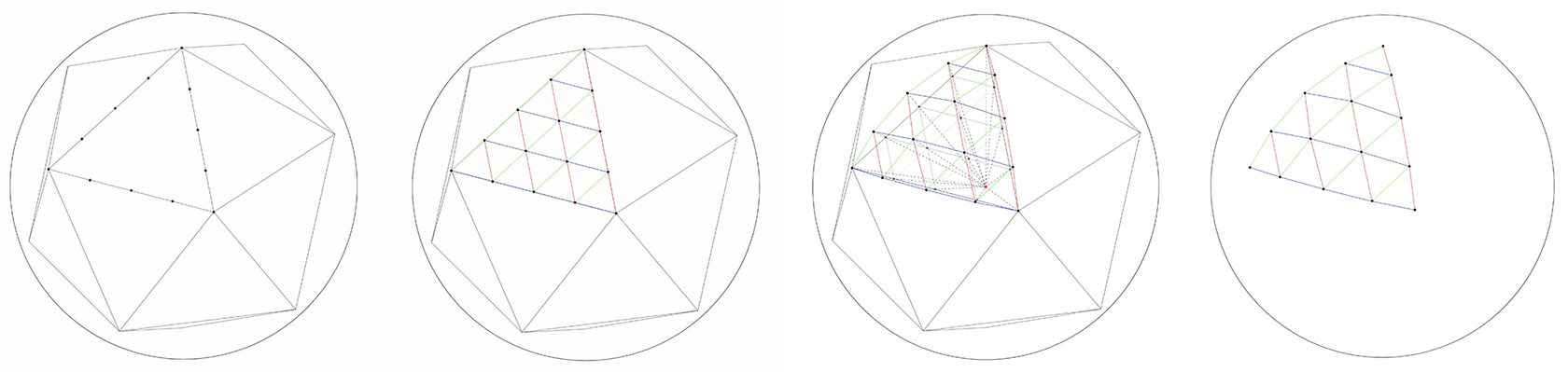
Построение сетчатого купола на основе проекции икосаэдра
ПОСТРОЕНИЕ ГЕОДЕЗИЧЕСКОГО КУПОЛА
Конструкция купола представляет собой деление сферического сегмента на треугольники посредством проекции икосаэдра. В искомую сферу вписывается икосаэдр, вершины которого лежат на поверхности сферы.
Далее производится деление каждой грани (треугольника) икосаэдра на равные части. Точки пересечения граней, вершины новых треугольников проецируются на поверхность искомой сферы. Спроецированные точки соединяются линиями - получение спроецированных треугольников. Процедура повторяется до достижения необходимого количества треугольников/необходимой длины стержней.
Для создания цифровой модели купола была разработана параметрическая модель в Rhino/Grasshopper, включающая в себя алгоритм подразделения сферы на множество треугольников.
Примечание:
Спроецированные треугольники неизбежно будут содержать несколько разных сторон и углов. Грани наименьшей длины (463 мм) будут находиться в узлах соединения вершин искомых треугольников, грани наибольшей длины (661 мм) — в центре. Длины элементов были определены Бауэрсфельдом математически и произведены на фабрике с точностью 1:10.000 длины стержня, что для строительной индустрии того времени было невиданным уровнем технического оснащения и качества.
Конструкция купола представляет собой деление сферического сегмента на треугольники посредством проекции икосаэдра. В искомую сферу вписывается икосаэдр, вершины которого лежат на поверхности сферы.
Далее производится деление каждой грани (треугольника) икосаэдра на равные части. Точки пересечения граней, вершины новых треугольников проецируются на поверхность искомой сферы. Спроецированные точки соединяются линиями - получение спроецированных треугольников. Процедура повторяется до достижения необходимого количества треугольников/необходимой длины стержней.
Для создания цифровой модели купола была разработана параметрическая модель в Rhino/Grasshopper, включающая в себя алгоритм подразделения сферы на множество треугольников.
Примечание:
Спроецированные треугольники неизбежно будут содержать несколько разных сторон и углов. Грани наименьшей длины (463 мм) будут находиться в узлах соединения вершин искомых треугольников, грани наибольшей длины (661 мм) — в центре. Длины элементов были определены Бауэрсфельдом математически и произведены на фабрике с точностью 1:10.000 длины стержня, что для строительной индустрии того времени было невиданным уровнем технического оснащения и качества.
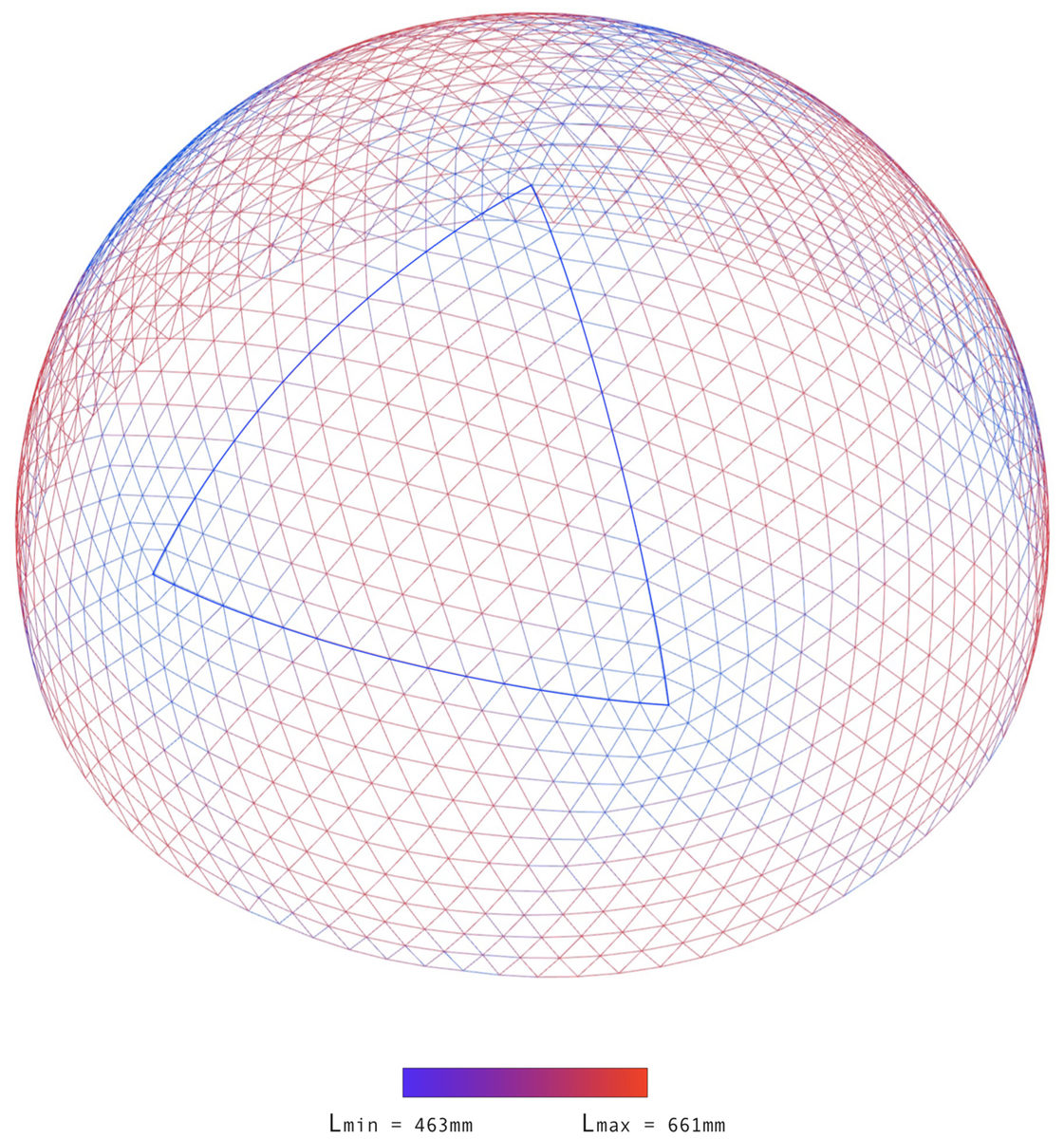
параметрическая модель длин элементов сетчатого купола
РАСЧЕТ ГЕОДЕЗИЧЕСКОГО КУПОЛА
После создания параметрической модели была собрана расчетная модель в Karamba 3D, чтобы проверить, как работает конструкция под действием различных нагрузок и как обеспечивается ее пространственная жесткость.
Определение усилий от снеговой нагрузки
Cправа представлена диаграмма напряжений от снеговой нагрузки. Для расчета было взято нормативное значение снеговой нагрузки для Йены (аналогично Берлину) находящейся на северо-германском плато, составляющее 0.85 kN/m2.
Интенсивность снеговой нагрузки по поверхности купола обычно принимают по закону р = р0 cos(φ), где p0 - равномерно распределенная нагрузка по проекции поверхности на горизонтальную плоскость.
Кольцевое усилие меняет знак при φ = 45°.
Диаграмма напряжений иллюстрирует этот принцип, подтверждая теоретические данные: действительно в верхней части купола все элементы подвержены сжатию, в то время как в нижней зоне в кольцевых (горизонтальных) элементах возникают растягивающие напряжения.
Максимальная деформация составляет 7 мм.
После создания параметрической модели была собрана расчетная модель в Karamba 3D, чтобы проверить, как работает конструкция под действием различных нагрузок и как обеспечивается ее пространственная жесткость.
Определение усилий от снеговой нагрузки
Cправа представлена диаграмма напряжений от снеговой нагрузки. Для расчета было взято нормативное значение снеговой нагрузки для Йены (аналогично Берлину) находящейся на северо-германском плато, составляющее 0.85 kN/m2.
Интенсивность снеговой нагрузки по поверхности купола обычно принимают по закону р = р0 cos(φ), где p0 - равномерно распределенная нагрузка по проекции поверхности на горизонтальную плоскость.
Кольцевое усилие меняет знак при φ = 45°.
Диаграмма напряжений иллюстрирует этот принцип, подтверждая теоретические данные: действительно в верхней части купола все элементы подвержены сжатию, в то время как в нижней зоне в кольцевых (горизонтальных) элементах возникают растягивающие напряжения.
Максимальная деформация составляет 7 мм.

Диаграмма напряжений купола под действием снеговой нагрузки. Karamba3D
Определение усилий от ветровой нагрузки
Усилия от ветровой нагрузки согласно литературе определяются приближенно путем замены действительной эпюры ветрового давления суммой двух эпюр: симметричной эпюры:
W1 = W0 cos*2φ,
и кососимметричной эпюры:
W2 = 0,5W0 sin*2φ sin*2φ,
где W0 — скоростной напор ветра.
То есть по формуле: W=W1+W2
Нормативное значение ветровой нагрузки для Йены, как и для Берлина, составляет W0= 0.39 кН/м2.
На диаграмме напряжений от ветровой нагрузки видно, что только малая часть купола подвержена деформации вовнутрь в наветренной стороны. Остальная часть купола подвержена выпучиванию наружу, так называемому «отсосу». В результате в значительной части конструкции возникают растягивающие напряжения.
Максимальная деформация составляет 7,2 мм.
Усилия от ветровой нагрузки согласно литературе определяются приближенно путем замены действительной эпюры ветрового давления суммой двух эпюр: симметричной эпюры:
W1 = W0 cos*2φ,
и кососимметричной эпюры:
W2 = 0,5W0 sin*2φ sin*2φ,
где W0 — скоростной напор ветра.
То есть по формуле: W=W1+W2
Нормативное значение ветровой нагрузки для Йены, как и для Берлина, составляет W0= 0.39 кН/м2.
На диаграмме напряжений от ветровой нагрузки видно, что только малая часть купола подвержена деформации вовнутрь в наветренной стороны. Остальная часть купола подвержена выпучиванию наружу, так называемому «отсосу». В результате в значительной части конструкции возникают растягивающие напряжения.
Максимальная деформация составляет 7,2 мм.

Диаграмма напряжений купола под действием ветровой нагрузки. Karamba3D
МАКЕТ
Фотографии макета: Юрий Пальмин
Благодарность
Особую благодарность хотелось бы выразить куратору выставки «Шухов. Формула Архитектуры», сотруднику Государственного музея архитектуры имени А.В. Щусева Марку Акопяну за проведение экскурсии по выставке, а также главному архитектору ГУМа Владимиру Камышникову, преподавателю МГСУ Юрию Южакову, доценту РГГУ Илье Печенкину и главному инженеру Metal Yapi Василию Анопченко за конструктивную критику по проектам.
Благодарность
Особую благодарность хотелось бы выразить куратору выставки «Шухов. Формула Архитектуры», сотруднику Государственного музея архитектуры имени А.В. Щусева Марку Акопяну за проведение экскурсии по выставке, а также главному архитектору ГУМа Владимиру Камышникову, преподавателю МГСУ Юрию Южакову, доценту РГГУ Илье Печенкину и главному инженеру Metal Yapi Василию Анопченко за конструктивную критику по проектам.
Источники
J. Krausse, Wissen in Bewegung - 80 Jahre Zeiss-Planetarium Jena, 2006
Дополнительная литература по теме
Vinyes Raso R., Integrating Aesthetics and Statics: A study of a Geodesic Dome, 2009
Ture Wester, Structural Order in Space, 1984
Горев В.В., Металлические конструкции, Том 2: Конструкции зданий, 2002 г.
J. Krausse, Wissen in Bewegung - 80 Jahre Zeiss-Planetarium Jena, 2006
Дополнительная литература по теме
Vinyes Raso R., Integrating Aesthetics and Statics: A study of a Geodesic Dome, 2009
Ture Wester, Structural Order in Space, 1984
Горев В.В., Металлические конструкции, Том 2: Конструкции зданий, 2002 г.